Die e(legante) Funktion - jetzt wirds genauer

Mithilfe der letzten Arbeitsblätter haben wir versucht, die Basis b der Funktion f(x) = b^x graphisch zu bestimmen ... was uns nur leider näherungsweise gelang. Nun wollen wir versuchen, die Basis b zu berechnen.

Ausgangspunkt für unsere Überlegungen sollen aus hier wieder die Funktionen g(x) = 2^x und h(x) = 3^x sein.

Aufgabe 1

Berechnen Sie mithilfe des Differentialquotienten 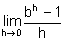die Ableitungen der Funktion f(x) = b^x für b = 2 und b = 3 jeweils an der Stelle x = 0. Interpretieren Sie die Ergebnisse.

b \ h	0,1	-0,1	0,01	-0,01	0,001	-0,001
2,0
3,0

Aufgabe 2

Anschaulich ist es klar, dass es genau eine reelle Zahl b gibt, so dass die Funktion f(x) = b^x an der Stelle x = 0 die Ableitung 1 hat, deren Graph im Punkt P(0|1) also die Steigung 1 besitzt. Nach den bisherigen Untersuchungen liegt diese besondere Zahl b zwischen 2 und 3.

Begründen Sie, dass für diese Zahl die Beziehung 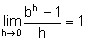gelten muss.

Diese Zahl erhält ein eigenes Symbol und einen eigenen Namen:

Definition
Diejenige Basis, für die die zugehörige Exponentialfunktion an der Stelle x = 0 die Ableitung 1 hat, für die also (b^x)’ = b^x gilt, wird mit dem Buchstaben e bezeichnet und heißt Eulersche Zahl. Es gilt also (e^x)’ = e^x.
L. Euler (1707-1783)

Welchen Wert hat die eulersche Zahl e?

Die Tangente an den Graphen der Funktion e^x muss per Definition im Punkt P(0|1) die Steigung 1 haben. Die Tangentengleichung in diesem Punkt lautet also y = x + 1.
In der Umgebung des Punktes P(0|1) schmiegt sich der Graph von e^x an diese Tangente an. Für betragsmäßig sehr kleine Werte von x, d. h. für x ≈ 0, gilt also e^x ≈ x + 1.
Die kleinen Werte für x und die Betrachtung x → 0 kann man algebraisch durchführen, indem die Substitution 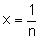vornimmt und den Grenzwert n → ∞ betrachtet, da 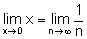gilt.
Mit dieser Substitution und der Näherung e^x ≈ x + 1 folgt die Beziehung 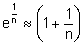. Potenziert man diese Beziehung mit n, so folgt (für sehr große n) 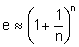. Aus dem „ungefähr gleich“ wird das gleich, wenn man den Grenzwert für n gegen unendlich berechnet. Es gilt also: .

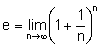Aufgabe 3

Setzen Sie für n die Zahlen 10, 100, 1000, 10000, ... ein und untersuchen Sie, wie sich die berechnete Wert für e ändert.

Die zur Basis e gehörige Exponentialfunktion erhält einen eigenen Namen.

Definition
Die Funktion f(x) = e^x nennt man die natürliche Exponentialfunktion. Möglich ist auch die Notation f(x) = exp(x).